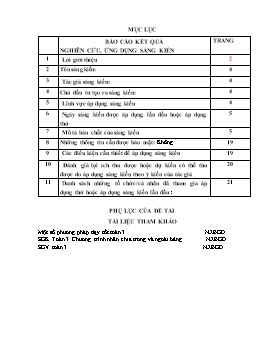
Sáng kiến kinh nghiệm Một số biện pháp giúp đỡ học sinh yếu kém khắc phục khó khăn khi giải các bài toán điển hình ở Lớp 3

uá trình giảng dạy có nhiều cố gắng đạt mục tiêu bài dạy, có ý thức nâng cao tay nghề.
	+ Xong việc vận dụng những kiến thức đã có vào việc giảng dạy còn có nhiều hạn chế, lúng túng, vụng về, thiếu linh hoạt.
	+ Năng khiếu sư phạm còn hạn chế dẫn đến việc hướng dẫn học sinh giải bài toán đôi khi còn thiếu chính xác. Kiến thức cơ bản nhiều khi còn bị lãng quên, sự đầu tư vào chuyên môn chưa nhiều dẫn đến chất lượng giờ dạy chưa cao.
	VD: Khi hướng dẫn học sinh giải toán, giáo viên chưa khuyến khích học sinh tìm nhiều cách giải khác nhau, chưa cho học sinh thấy được ý nghĩa thực tiễn của nó trong cuộc sống.
	+ Một số giáo viên còn chịu ảnh hưởng của phương pháp dạy học truyền thống.
7.2. 3. Thực trạng việc học giải toán điển hình của học sinh lớp 3	
	Trong khi nghiên cứu đề tài này tôi đã điều tra đối chứng hai lớp 3 của trường tiểu học Chấn Hưng – Vĩnh Tường – Vĩnh Phúc. Tôi nhận thấy học sinh yếu, kém giải toán có lời văn có nội dung hình học và bài toán liên quan đến rút về đơn
vị hay mắc phải sai lầm như sau:
Bài toán có lời văn có nội dung hình học
	- Học sinh chưa đọc kỹ đề bài, xác định yêu cầu bài toán chưa đúng, không biết bài toán thuộc loại toán nào dẫn đến việc áp dụng công thức, quy tắc nhầm, lẫn lộn với nhau, kết quả giải toán bị sai.
	+ Khi bài toán yêu cầu tính chu vi hình chữ nhật thì lại áp dụng quy tắc tính chu vi hình vuông và ngược lại khi bài toán yêu cầu tính chu vi hình vuông thì lại áp dụng quy tắc quy tắc tính chu vi hình chữ nhật.
	+ Khi bài toán yêu cầu tính chu vi hình vuông và chu vi hình chữ nhật thì học sinh yếu, kém không nắm chắc quy tắc để vận dụng quy tắc tính, nhầm giữa tính chu vi hình vuông sang tính diện tích hình vuông, nhầm giữa tính chu vi hình chữ nhật sang tính diện tích hình chữ nhật.
	+ Trong bài giải bài toán về chu vi, diện tích các hình (Bài 3 trang 155- Toán 3) khi viết tên đơn vị đo, các em còn bỏ sót, nhầm lẫn. Thông thường kích các cùng đơn vị đo nào thì chu vi có cùng đơn vị đo đó, nhưng với diện tích thì đơn vị đo lại khác. Chẳng hạn: Với hình chữ nhật có chiều dài 9 cm, chiều rộng 6 cm thì đơn vị đo của chu vi là cm, nhưng đơn vị đo của diện tích là cm2. Cụ thể là:
Chu vi hình chữ nhật là:
(9 + 6 ) x 2 = 30 (cm)
Diện tích hình chữ nhật là:
9 x 6 = 54 (cm2)
	+ Trong trường hợp số đo các cạnh không cùng đơn vị thì học sinh chưa biết đổi ra cùng đơn vị đo.
	VD: Tính diện tích và chu vi hình chữ nhật có chiều dài là 4 dm, chiều rộng là 8 cm.
	- Học sinh yếu kém nhận diện hình chậm, không hiểu thuật ngữ toán học, không biết bài đã cho dữ kiện nào để áp dụng vào giải toán. Không nắm được các thao tác giải toán, không biết tư duy bài toán (bằng lời hoặc hình vẽ) nên trình bày sai lời giải, sai bài toán, đáp số sai, thiếu.
	- Học sinh yếu còn nhầm khi bài toán cho chu vi hình vuông đi tìm cạnh, học sinh không hiểu bài toán ngược lại áp dụng công thức cạnh hình vuông bằng chu vi chia cho 4.
	- Ngoài ra còn một số bài toán đòi hỏi học sinh phải tư duy tìm các công thức đã cho để giải. Khả năng giải bài toán mang tính chất tồng hợp kiến thức của các em còn kém, các em quên mất kiến thức cũ liên quan nên giải bài toán bị sai.
	VD: Bài toán
	+ Cho cạnh hình vuông tính chu vi và diện tích, học sinh nhầm giữa hai cách tính nên kết quả bị sai.
+ Cho chiều dài, chiều rộng hình chữ nhật. Tính chu vi, diện tích. Học sinh lại nhầm hai công thức tính dẫn đến kết quả sai.
Bài toán liên quan đến rút về đơn vị
Dạng 1
+ Bước 1: Rút về đơn vị, tìm giá trị một phần
- Học sinh nhầm khi trả lời chưa rõ ràng
	- Sau khi thực hiện phép tính chia ghi danh số sai với câu trả lời
	VD: Bài 2 trang 128
	“Có 28 kg gạo đựng đều trong 7 bao. Hỏi 5 bao có bao nhiêu ki-lô-gam gạo?”
	Học sinh trả lời sai:
Danh số kết quả sau: 28 : 7 = 4 (bao)
Học sinh phải làm đúng là: 28 : 7 = 4 (kg)
Bước 2: Tìm 5 bao có số ki-lô-gam gạo là:
4 x 5 = 20 (kg)
	Học sinh hay đặt ngược phép tính là:
5 x 4 = 20 (bao)
	Như vậy:
	Khi học sinh giải bài toán dạng 1 hay trả lời sai hoặc sai danh số, phép tính sai vì đặt ngược.
	Dạng 2:
	Bước 1: Tìm giá trị một phần thực hiện phép chia
	Bước 2: Biết giá trị một phần thực hiện phép chia để tìm kết quả theo câu hỏi của bài toán.
	- Học sinh thường sai: Trả lời sai, ghi danh số nhầm
	VD: Bài toán 2 trang 166
	Bước 1: tìm giá trị một phần
	- Học sinh trả lời sai
7.2. 4. Một số nguyên nhân dẫn đến thực trạng trên
	a. Nguyên nhân khách quan
	- Do đặc thù tình hình của địa phương là vùng đất nông nghiệp 90% học sinh là con em nông dân trong đó có đến 50% là con nông dân nghèo, điều kiện 
kinh tế gia đình eo hẹp dẫn đến điều kiện học tập của các em cũng bị ảnh hưởng rất nhiều.
	- Một số gia đình chưa thực sự quan tâm động viên các em kịp thời cũng như tạo điều kiện tốt hơn để các em học tập.
	b. Nguyên nhân chủ quan
	- Giáo viên: Trong giảng dạy, một số giáo viên vận dụng các phương pháp dạy học chưa linh hoạt, nhịp độ giảng dạy quá nhanh khiến học sinh yếu, kém không theo kịp. Một số giáo viên còn thiếu tinh thần trách nhiệm với học sinh. Việc đầu tư cho chuyên môn nghiệp vụ còn hạn chế, chưa nắm vững yêu cầu về kỹ thuật và kỹ năng của bài toán, chưa quan tâm đến học sinh yếu, kém.
	- Học sinh:
	+ Sự phát triển nhận thức của một số em còn chậm, không đồng đều, hoạt động tư duy logic kém. Việc lĩnh hội kiến thức ở các lớp trước chưa đầy đủ, còn những lỗ hổng về kiến thức. Một số em có thái độ học tập chưa tốt, ngại cố gắng, thiếu tự tin.
	+ Ngoài ra, có em do sức khỏe chưa tốt, gia đình chưa quan tâm đến việc học hành của các em. Một số phụ huynh do không nắm được cách giải toán ở tiểu học nên không hướng dẫn được cho các em hoặc hướng dẫn các em những cách giải toán của bậc Trung học cơ sở.
	Có rất nhiều nguyên nhân ảnh hưởng đến kết quả dạy và học xong đây chỉ là một số nguyên nhân mà trong chương trình công tác và nghiên cứu làm đề tài tôi phát hiện ra. Những nguyên nhân trên tác động lẫn nhau làm giảm hứng thú học tập của học sinh, làm cho cac em thiếu tự tin cố gắng vươn lên dẫn đến kết quả học tập không tốt.
	Để khắc phục những tồn tại trên cần phải có biện pháp khắc phục hợp lí.
7.3. CÁC GIẢI PHÁP KHẮC PHỤC
	Việc dạy học gải toán ở tiểu học là giúp học sinh tự tìm hiểu được mối quan hệ giữa cái đã cho và cái phải tìm, mô tả quan hệ đó bằng cấu trúc ghép tính cụ thể, thực hiện phép tính, trình bày lời giải bài toán. Giáo viên cần phải tổ chức cho học sinh nắm vững khái niệm toán học, cấu trúc phép tính, các thuật ngữTổ chức cho học sinh thực hiện các bước giải toán. Vậy qua quá trình nghiên cứu thực hiện đề tài tôi xin đưa ra một số biện pháp sau đây.
7.3. 1. Trang bị những công thức, quy tắc, kỹ năng giải toán
	Đây là vấn đề vô cùng quan trọng trong việc truyền tải kiến thức cho học sinh, thay thế cho việc giáo viên áp đặt kiến thức cho học sinh buộc học sinh phải thuộc lòng những điều giáo viên thuyết trình (phương pháp dạy học truyền thống) bằng việc giáo viên là người dẫn dắt các em tự mình tìm tòi khám phá kiến thức mới (phương pháp dạy học tích cực). Trong quá trình giảng dạy giáo viên cần vận dụng triệt để biện pháp này vì học sinh muốn giải được các bài toán thì cần phải được trang bị đầy đủ những kiến thức có liên quan đến việc giải toán mà những kiến thức này chủ yếu được cung cấp qua các tiết lý thuyết. Do vậy dưới sự dẫn dắt của giáo viên, học sinh cần tìm ra được cách giải bài toán và cần phải được chính xác hóa nhờ sự giúp đỡ của giáo viên. Qua quá trình tự tìm tòi, khám phá kiến thức mới dựa trên những cái đã biết giúp các em hiểu sâu hơn, nhớ lâu kiến thức ấy hơn nếu như tự mình tìm ra kiến thức ấy
	Học sinh cần nắm chắc quy tắc, công thức tính, các bước tính của một phép tính từ đó mới rèn luyện được kỹ năng tính toán.
	Đối với loại toán có nội dung hình học thì khả năng nhận biết các đặc điểm cảu một hình vẽ là rất quan trọng.
	Ví dụ:	 Khi dạy về “Diện tích hình chữ nhật” giáo viên cần cho học sinh nhắc lại đặc điểm của hình chữ nhật thông qua hình vẽ.
+ Khả năng cắt ghép hình tam giác thành hình chữ nhật.
	+ Giáo viên cần có biện pháp giúp học sinh nhớ rõ các ký hiệu hình vẽ. 
Chẳng hạn, đâu là cạnh chiều dài của hình, đâu là cạnh chiều rộng của hình chữ nhật. Từ đó học sinh biết vận dụng vào giải các bài toán áp dụng trực tiếp quy tắc đã xây dựng để vận dụng tính.
	Bài tập VD: Cho hình chữ nhật có cạnh dài là 8cm, cạnh ngắn là 5cm. Tính diện tích hình chữ nhật đó ?
	Với bài tập này học sinh chỉ cần vận dụng đúng quy tắc, công thức đã được trang bị là giải được ngay. Cũng có những bài toán đòi hỏi học sinh phải có khả năng tư duy thì mới giải được. Do vậy, giáo viên cần rèn cho các em kỹ năng này.
	VD: Bài toán: Cho hình chữ nhật có nửa chu vi là 22cm, cạnh ngắn là 9 cm. Tính diện tích hình chữ nhật đó ?
	- Khi giải bài toán không có cùng đơn vị đo thì phải biết đổi ra cùng một đơn vị đo.
	VD: Số đo cạnh theo mm, số đo diện tích theo cm2. Vậy phải đổi số đo cạnh ra cm.
	- Giáo viên cần lưu ý cho học sinh:
	+ Với hình chữ nhật có số đo chu vi là cm, thì đơn vị đo của diện tích là cm2
	+ Với hình vuông có số đo chu vi là cm thì đơn vị đo của diện tích hình vuông là cm2.
*Với bài toán liên quan đến rút về đơn vị:
	 Giáo viên cần hướng dẫn cho học sinh biết đề bài yêu càu tính cái gì? Bài toán thuộc dạng 1 hay dạng 2 để giải bài toán.
	Ví dụ:
	+ Bài toán ở dạng 1 thì phải tìm giá trị của một phần là thực hiện phép chia rồi mới tìm được giá trị của nhiruf phần (thực hiện phép tính nhân).
	+ Bài toán chia ở dạng 2 thì: Bước 1 cũng phải tìm giá trị một phần (thực hiện phép tính chia) nhưng ở bước 2 thì lại khác với bước 2 ở dạng 1 đó là biết giá trị một phần rồi lại tiếp tục thực hiện phép chia để tìm kết quả theo yêu cầu của bài toán.
	*Điều quan trọng chủ yếu khi dạy giải toán là dạy học sinh biết cách giải bài toán (phương pháp giải toán). Giáo viên không được làm thay, không được áp đặt cach giải cần phải tạo cho học sinh tự tìm ra cách giải bài toán tập trung vào 3 bước:
	+ Tính toán để biết bài toán cho gì, hỏi gì, yêu cầu gì?
+ Tìm cách giải thông qua việc thiết lập mối quan